23 مارس 2023 -توسط باب یرکا،
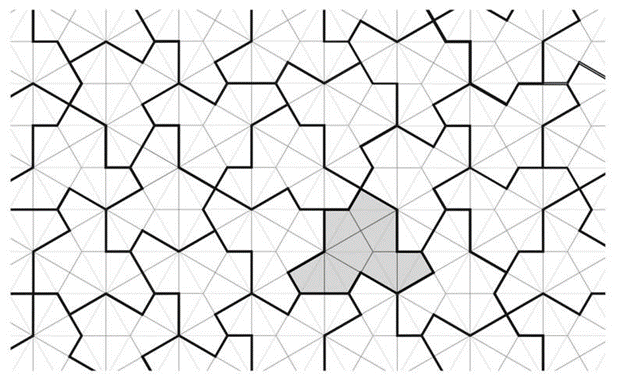
کاشی پلیکیت «کلاهی» خاکستری یک «انیشتین» است، یک سطح تکتکه غیرپریودیک. به عبارت دیگر، کپیهایی از این کاشی ممکن است در کاشیکاریهای صفحه مونتاژ شوند . اما کپیهایی از کاشی نمیتوانند کاشیکاریهای تکراری را تشکیل دهند، کاشیهایی که دارای تقارن تکرار هستند. در واقع، کاشی به طور غیرقابل شمارشی تعداد زیادی بلوک را می پذیرد. اعتبار: arXiv (2023).
گروهی از ریاضیدانان از دانشگاه یورکشایر، دانشگاه کمبریج، دانشگاه واترلو و دانشگاه آرکانزاس یک شکل هندسی دوبعدی را کشف کرده اند که وقتی کاشی کاری می شود، خود را تکرار نمی کند. دیوید اسمیت، جوزف ساموئل مایرز، کریگ کاپلان و چایم گودمن استراوس مقالهای نوشتهاند که چگونه شکل منحصر به فرد و کاربردهای احتمالی آن را کشف کردهاند. مقاله کامل آنها در سرور preprint arXiv موجود است.
هنگامی که افراد کف محل خود را کاشی می کنند، تمایل دارند از اشکال هندسی ساده استفاده کنند که خود را به الگوهای تکراری مانند مربع یا مثلث می رساند. با این حال، گاهی اوقات، مردم الگوهایی را می خواهند که تکرار نمی شوند، اما در صورت استفاده از همان نوع شکل، چالشی را نشان می دهند. در این تلاش جدید، تیم تحقیقاتی یک شکل هندسی منفرد را کشف کرده اند که اگر برای کاشی کاری استفاده شود، الگوهای تکراری تولید نمی شود.
در سناریوی خود، محققان خاطرنشان کردند که کاشی کاری به اتصال اشکال به یکدیگر اشاره دارد به طوری که هیچ همپوشانی یا شکافی وجود نداشته باشد. کاشیکاریهایی که الگوهای تکرار شونده ندارند به عنوان کاشیکاری نامتناوب شناخته میشوند و عموماً با استفاده از چندین شکل کاشی به دست میآیند. سالهاست که ریاضیدانان ایده ایجاد اشکالی را مطالعه میکنند که میتوان از آنها برای ایجاد تنوع بینهایتی از الگوها هنگام کاشیکاری استفاده کرد.
یکی از اولین تلاش ها منجر به مجموعه ای از 20426 کاشی شد. در سال 1974، کاشیهای Penrose ساخته شدند که در مجموعهای از دو لوزی با شکلهای متفاوت عرضه میشوند. از آن زمان، ریاضیدانان به جستجوی آنچه که به عنوان شکل «انیشتین» معروف شده است، ادامه داده اند – شکلی که می تواند به تنهایی برای کاشی کاری های دوره ای استفاده شود.
قابل ذکر است که این نام از عبارت “یک سنگ” در آلمانی گرفته شده است، نه از فیزیکدان معروف. در این تلاش جدید، گروه تحقیقاتی ادعا می کند که شکل گریزان انیشتین را یافته اند و آن را به صورت ریاضی ثابت کرده اند.
شکل دارای 13 ضلع است و تیم از آن به سادگی به عنوان “کلاه” یاد می کند. آنها آن را ابتدا با تجزیه احتمالات با استفاده از رایانه و سپس با مطالعه مجموعه های کوچکتر به دست آمده با دست پیدا کردند. هنگامی که آنها احتمال خوبی را به دست آوردند، آن را با استفاده از یک برنامه نرمافزار ترکیبی آزمایش کردند – و با اثبات غیر تناوبی شکل با استفاده از یک استدلال غیرقابل مقایسه هندسی، آن را آزمایش کردند. محققان با پیشنهاد این نکته پایان میدهند که محتملترین کاربرد کلاه در هنر است.







